
BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 2장: 최소 제곱
2장 : 최소 제곱 모델 최소 제곱 모델(=OLS) 정의 1) 개념: 목표값과 본 모델에서 도출되는 예측값을 이용해 정의한 비용 함수가 평균 제곱 오차 (MSE)인 모델 → 예측값과 목표값의 차이인 잔차 제곱
sol-butter1472.tistory.com
2장 : 최소 제곱 모델
BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 3장: 로지스틱
BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 2장: 최소 제곱 2장 : 최소 제곱 모델 최소 제곱 모델(=OLS) 정의 1) 개념: 목표값과 본 모델에서 도출되는 예측값을
sol-butter1472.tistory.com
3장 : 로지스틱 회귀 모델
4장 : 라쏘 모델
피처 선택법
- 필터 기반 선택법
- 래퍼 기반 선택법
-임베디드
1) 필터 기반 선택법
- 단일 피처를 대상으로 피처를 선택하는 방법이다.
- 분석에 좋은 피처만 포함하고자 기준을 정하고 해당 기준을 만족하는 피처만 모델에 포함
- 수치형 변수- 상관계수 기반 필터
- 범주형 변수- 카이제곱 기반 필터

해당 코드를 통해 64개의 피처 중 20개의 피처를 선택한 것을 확인할 수 있다.
SelectKBest 객체의 get_support() 메서드로 칼럼 위치를 선택할 수 있으며
이렇게 선택한 피처를 다시 데이터 프레임 형태로 저장할 수 있다.
2) 래퍼 기반 피처 선택법
전진 선택법은 sklearn.feature_selection.RFE 클래스를,
sklearn.feature_selection.SequentialFeatureSelector 클래스로는 전진 선택법과 후진 소거법을 둘 다 제공한다.
책에서는 RFE 클래스를 중점으로 다루고 있음으로 RFE 클래스를 중점으로 소개하겠다.
| 하이퍼파라미터 | 주요값 | 기본값 | 의미 |
| estimator | Estimator 객체 | - | 특성 선택에 사용할 모델 지정 선형 모델 트리 기반 모델 사용 |
| n_features_to_select | int, 0<float<1, None |
None | 선택할 피처 개수 혹은 비율 -None: 피처의 절반이 선택 -int: 선택할 피처 개수 -float: 선택할 피처 수의 비율 |
| step | int>= 1, 0<float< 1 |
1 | 각 이터레이션에서 제거할 피처 개수 혹은 비율 -int: 각각의 이터레이션에서 제거할 피처 개수 - float: 각각의 이터레이션에서 제거할 피처의 비율 |
이외 Verbose 하이퍼파라미터가 존재한다. 이는 학습 중에 로그를 출력할지의 여부를 결정해준다.
3) 임베디드
원 핫 인코딩과 희소 데이터셋

원 핫 인코딩:
원 핫 인코딩은 범주형 변수를 수치형 변수로 변환하여 활용하는 방법이다.
pandas 패키지의 get_dummies() 함수를 통해 변환이 가능하다.
희소 데이터셋:
범주형 변수가 a개의 레이블로 구성되고 b개의 샘플을 가지고 있다고 해보자.
이때 원 핫 인코딩 적용 후 행렬 원소의 수는 axb이나 그중 0이 아닌 값을 가지는 원소는 a개밖에 없으므로 1/a의 비율만 값이 존재하고 나머지는 0으로 채워지는데 이것을 희소 데이터셋이라고 한다.
고유한 단어의 수가 많은 텍스트 분석에서 희소 데이터셋은 더 많이 발생한다.
좋은 모델이란?
머신러닝에서 가장 중요한 사실은 모델의 성능이다.
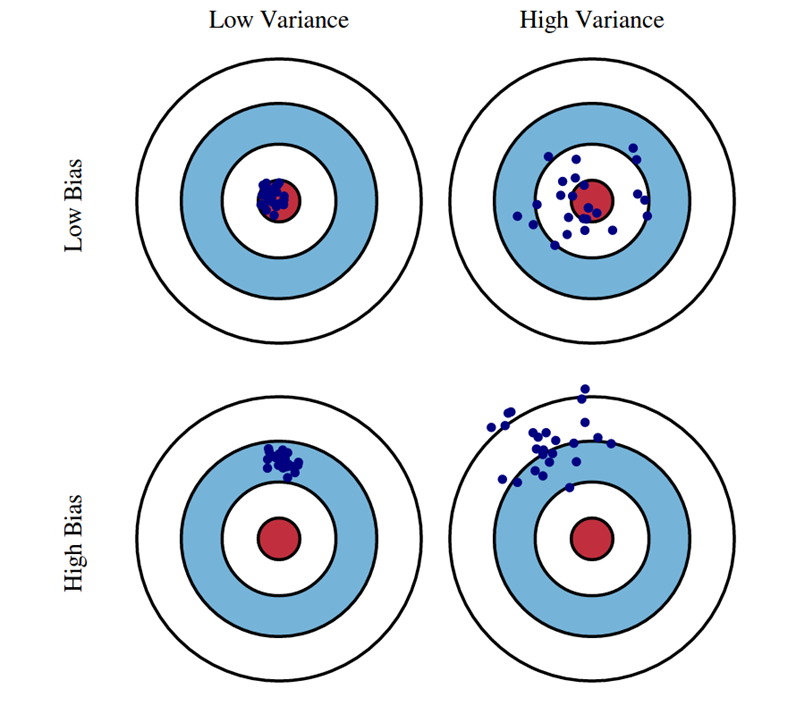
bias와 variance가 낮은 모델이 정답에 근접한 사실을 알 수 있다.
정규화
정규화는 결국 모델의 성능을 높이는 중요한 과정이다.
(라쏘 모델)
Least Absolute Shrinkage and Selection Operator
- shrinkage는 회귀계수 파라미터 값이 작아지는 것을 의미
- y를 예측할때 중요한 x값을 자동으로 선택하는 기능까지 있는 모델
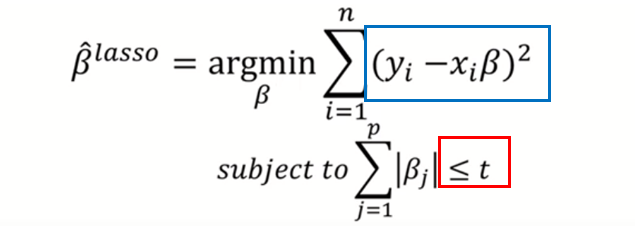
릿지와 거의 비슷하다. 라쏘는 절댓값을 beta값에 절댓값을 취한다는 특징이 있다.

t(제약조건)를 작게할 수록 제약이 크다. 즉 람다를 작게 설정했다고 볼 수 있겠다.
결국 람다는 하이퍼파라미터이고, 람다를 어떻게 설정하는지가 우리가 생각해야 할 문제이다.

람다를 크게 설정하거나 작게 설정했을 때 발생할 수 있는 일들이다.
너무 작게 설정해도 크게 설정해도 모델의 성능은 떨어지기 마련이므로
적절하게 람다값을 설정하는 것이 중요하다고 볼 수 있다.
람다가 0이면 mse와 똑같아진다.
람다가 무한대면 제약을 매우 강하게 되는 것 즉 constant y^이 나온다.

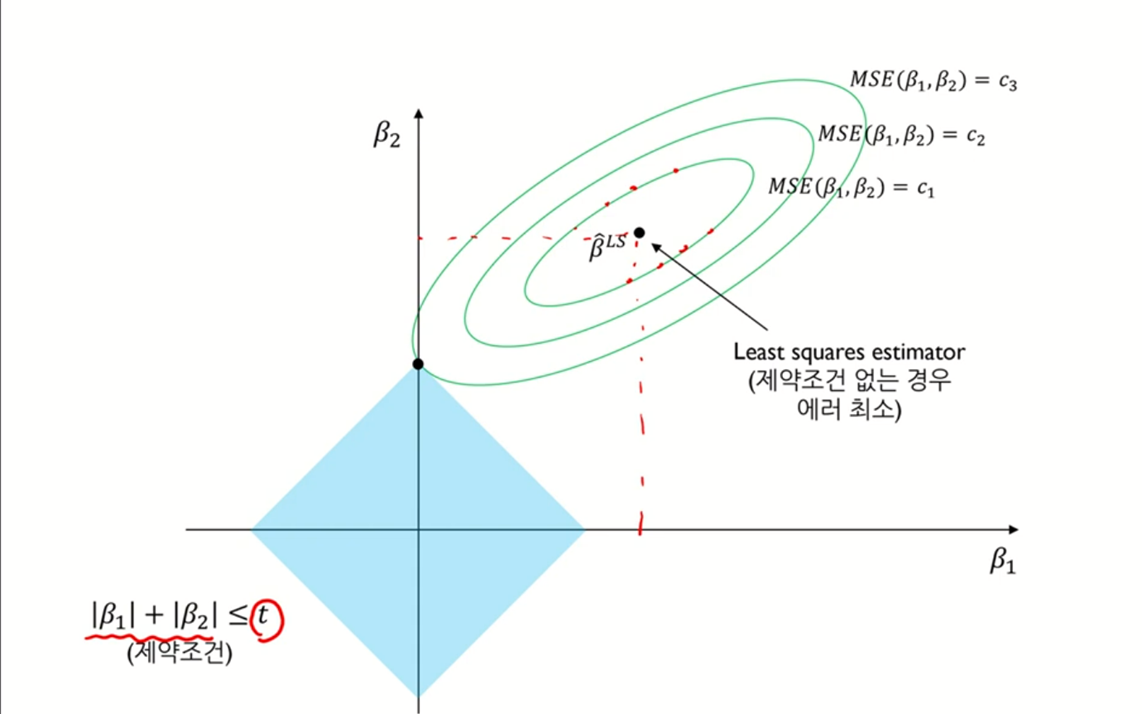
왼쪽은 릿지 모델, 오른쪽은 라쏘 모델을 표현한 그림이다.
릿지 모델은 beta값을 제곱으로 설정하므로 동그라미의 형태로 그려진다.
반면, 라쏘 모델은 절댓값을 취한다는 점에서 마름모의 형태로 제약조건이 그려지는 것을 확인할 수 있다.
라쏘 모델은 미분이 불가능하기 때문에 수치 최적화 방법을 활용한다.
수치 최적화 방법론으로는
- quadratic programming
- LARS
- coordinate descent 알고리즘
을 사용한다. 책에서는 coordinate descent를 활용했으므로 좌표 하강법을 중심으로 설명한다.


릿지 모델과 라쏘 모델의 차이는 다음과 같다.
라쏘는 결정적으로 변수 간 상관관계가 높은 상황에서는 예측 성능이 떨어진다는 단점이 있다.(이를 해결하고자 나온 것이 엘라스틱 넷. 릿지와 라쏘를 결합한 모델)
그럼에도 라쏘는 제약을 많이 가하면 예측에 중요하지 않은 변수가 더 빠르게 감소,
즉 t(제약조건)가 작아짐에 따라 예측에 중요하지 않은 변수가 0이 되기 때문에 내가 필요한 피처들만 가지고 예측할 수 있다는 장점이 있다.
좌표 하강법
좌표 하강법은 한 번에 하나의 변수만을 고려하므로 계산이 상대적으로 더 간단함.
좌표 하강법 이용한 라쏘 모델 구현
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.datasets import load_diabetes
%matplotlib inline
#당뇨병 데이터셋 이용 및 평균 중심화 수행
diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target
y = y - y.mean()
#soft_threshold()함수와 좌표 하강법 알고리즘 구현
def soft_threshold(rho,alpha):
if rho < -alpha:
return rho + alpha
elif rho > alpha:
return rho - alpha
return 0
def coordinate_descent_lasso(X,y, alpha = .01, num_iters = 100):
n, p = X.shape
w = np.ones((p,))
z = np.zeros((p,))
for j in range(p):
X_j = X[:,j].reshape(-1,1)
z[j] = np.inner(X[:,j],X[:,j])/n
for i in range(num_iters):
for j in range(p):
rho = np.inner(X[:,j], y-np.matmul(X,w)+w[j]*X[:,j])/n
w[j] = 1 / z[j]*soft_threshold(rho,alpha)
return w.flatten()
ws = []
alphas = np.logspace(-3,1,300)
for alpha in alphas:
w = coordinate_descent_lasso(X, y, alpha=alpha, num_iters = 100)
ws.append(w)
w_lasso = np.stack(ws).T
plt.figure(figsize =(12,8))
for i in range(w_lasso.shape[0]):
plt.plot(alphas, w_lasso[i],label = diabetes.feature_names[i])
plt.xscale('log')
plt.xlabel('Log alpha')
plt.ylabel('Parameter')
plt.title('Lasso Path')
plt.legend()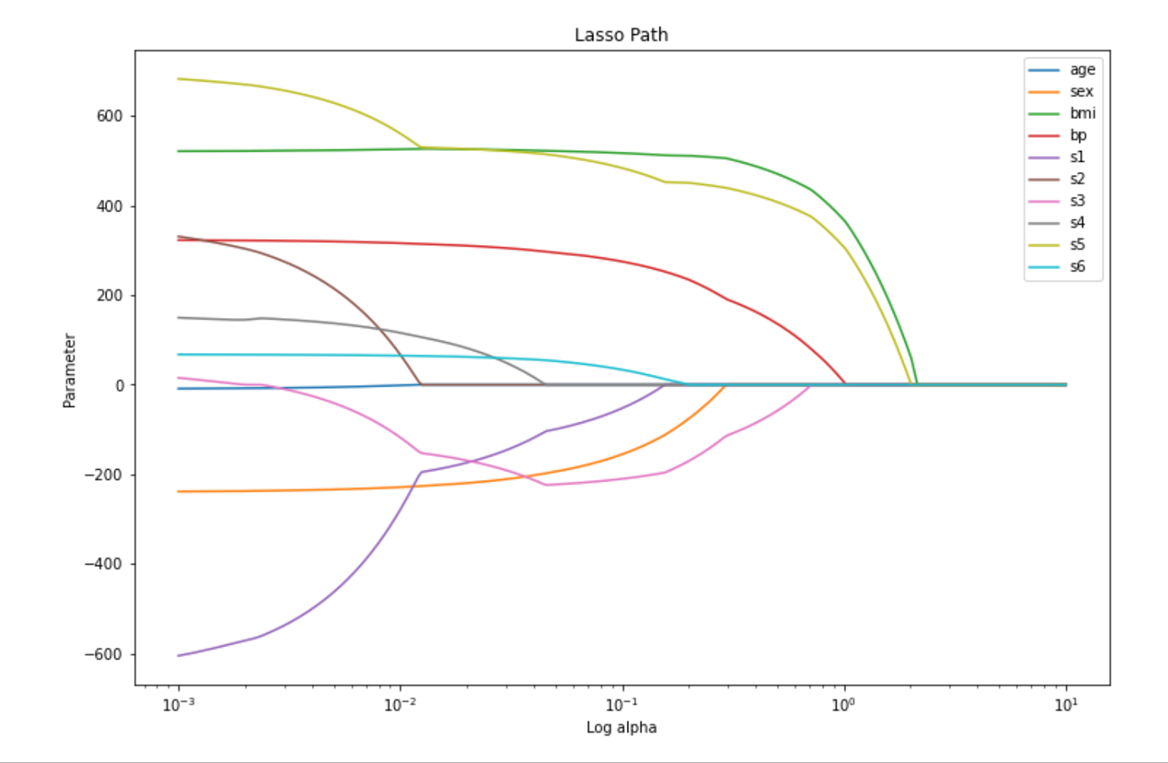
알파값이 커짐에 따라 점점 더 많은 파라미터가 0으로 감쇄하는 것을 확인할 수 있다.
패키지로 표현하기
1) 라쏘 클래스 내 하이퍼 파라미터
| 하이퍼파라미터 | 주요값 | 기본값 | 의미 |
| alpha | float > 0 | 1.0 | L1규제 패널티 계수로, 비용 함수에서의 알파 해당, alpha가 0에 가까워질수록 OLS해에 수렴 |
| fit_intercept | bool | True | 절편 포함 여부 결정 - True: 절편 포함 |
| max_iter | int > 0 | 1000 | 이터레이션 횟수의 상한선 |
| tol | float > 0 | 1e-4 | 조기 종료에 대한 허용 오차. 이터레이션에 따른 업데이트의 값이 tol보다 작을 때 추가 조건을 확인하고 조기 종료를 결정 |
| positive | bool | False | 파라미터 제약 조건 - True: 모든 파라미터가 0 이상의 값을 가지도록 강제 |
| selection | 'cyclic', 'random' |
'cyclic' | 계수의 업데이트 방식 - 'cyclic' : 정해진 순으로 계수 업데이트 -'random': 매 이터레이션에서 계수를 랜덤한 순서로 업데이트. 이 옵션을 선택시 특정 조건에서 수렴 속도가 매우 빨라질 수 있다. |
| random_state | None, int | None | selection이 'random' 일때 랜덤성을 제어하고자 사용 |
2) Lasso 클래스 사용하기

당뇨병 데이터셋을 라쏘 모델로 학습했다.
피처의 스케일링을 pipeline으로 진행 후
학습 결과, 학습 데이터셋보다 테스트 데이터셋의 MAE 크기가 약 1.3 정도 작은 것을 확인.
reg.coef_ 어트리뷰트 출력으로 10개의 피처 중 4개의 피처만 예측에 사용되었음을 확인할 수 있었다.
모델 선택법
- 가능한 여러 가지 경쟁 모델 중 가장 적절한 모델 선택하는 방법
- 학습한 모델의 평가를 어떻게 할 것인지 고르는 방법
- 샘플 내 기준과 샘플 외 기준으로 모델의 기준이 나뉨
- 샘플 내 기준: 결정 계수 R^2, 아카이케 정보 기준, 베이즈 정보기준
- 샘플 외 기준: 교차검증법
1) AIC (아카이케 정보 기준)와 BIC(베이즈 정보 기준)
2) 차이
3) 교차 검증법
1개를 검증에 사용하는 방식을 k개 경우의 수에 대해 각각 적용하고 이의 평균 성능을 산출하는 방법
-> 쉽게 말해 데이터를 여러 개 쪼개어, 모델을 학습하고 평가하는 과정을 반복하는 것


AIC와 BIC로 하이퍼파라미터 튜닝 수행과 교차 검증법으로 하이퍼파라미터를 수행한 모습
AIC와 BIC를 기준으로 한 결과보다 교차 검증법이 더 오래 걸린다는 것을 알 수 있었다.
교차 검증법은 학습 데이터 밖의 데이터를 기준으로 검증이 이루어지므로 정보기준보다 기본적으로 많은 시간이 필요하다.
'공부' 카테고리의 다른 글
| 오차역전파 (0) | 2023.12.29 |
|---|---|
| BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 5장 : 릿지 회귀 모델 (0) | 2023.12.11 |
| BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 3장: 로지스틱 회귀 모델 (0) | 2023.12.11 |
| BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 2장: 최소 제곱 모델 (0) | 2023.12.11 |
| 실전 머신러닝 1장 데이터셋 분할/데이터 전처리 (0) | 2023.12.07 |