
사전지식 : 거리 메트릭
거리 메트릭(distance metric)
: 공간에서 두 점 사이의 거리를 측정하는 방법이나 함수를 나타낸다.
민코프스키 메트릭(Minkowski metric)
: 유클리드 거리와 맨허탄 거리를 표현하는 일반적인 형태


유클리드 거리(Euclidean distance)
p=2 일때
흔히 생각하는 두 점 사이의 거리

맨해튼 거리(Manhattan distance)
p=1 일때
좌표 평면에 평행한 방향으로 갈때의 최솟값
대각선이 아닌 수평선과 수직선으로만 이동하여 계산된 거리


K-최근접 이웃 모델(K-NN)
지도학습에 사용되는 간단하면서도 효과적인 알고리즘 중 하나
파라미터를 따로 학습하지 않음 (비모수적 모델)
데이터 특성이 적고 명확한 경우에 유리
화이트 박스 모델
예측 방법
1)새로운 데이터가 주어졌을 때, 해당 데이터와 가장 유사한 K개의 이웃을 찾음
2) 이 이웃들의 레이블 또는 값을 사용하여 새로운 데이터 포인트의
클래스를 할당함
3) 분류 문제라면, 이 이웃들의 레이블 중 다수결 투표를 통해 예측
회귀 문제라면, 평균 또는 가중 평균을 통해 예측
완전 탐색 알고리즘
가능한 모든 경우의 수를 조사하여 원하는 결과를 찾는 알고리즘 기법
모든 학습 데이터에 대한 거리를 계산 후 거리 순으로 정렬하여
가장 가까운 K개를 얻음
K 설정하기
최근접 이웃의 수 K 설정이 핵심
K 가 클수록 노이즈(분산)감소, 클래스의 결정 경계가 단순해 짐
다양한 하이퍼 파라미터 최적화 기법으로 선택 가능
이진 분류 -> K는 홀수! 다중 클래스 분류라면?
KNN 모델의 심화 이론
다음의 하이퍼 파라미터를 추가로 조절하여 모델을 최적화
거리 메트릭과 가중치
거리 메트릭에 따라서 다양한 결과 도출 (주로 유클리드 거리 사용)
가까운 이웃에는 더 큰 가중치를 부여 -> 거리의 역수에 해당하는 가중치 곱
클래스 가중치
목표 클래스에 불균형이 있다면 클래스별로 가중치를 다르게 설정
알고리즘 개선
완전 탐색 알고리즘 : 데이터 수 증가 ~ 비효율성 증가
트리 기반 데이터 구조 제안 : 시간 복잡도

KD 트리
이진 탐색 트리를 K차원 데이터에 적용하도록 확장한 자료 구조
각 레벨마다 데이터를 한 축(차원)을 기준으로 분할

Ball 트리
데이터 포인트를 구에 담거나 구를 중심으로 데이터를 분할하여 트리를 형성
KNN 분류 모델 구현하기
Data Split

Creating a Function

Model Evaluation

패키지로 표현하기
학습 및 예측 시간 비교
학습 시간
KNN 회귀 < 결정 트리 회귀 < OLS
OLS와 결정 트리 회귀는 피처 개수에 영향을 받음
예측 시간
결정 트리 회귀와 OLS는 0에 근사
KNN 회귀는 예측에 걸리는 시간이 압도적으로 높음
KNN 회귀 모델
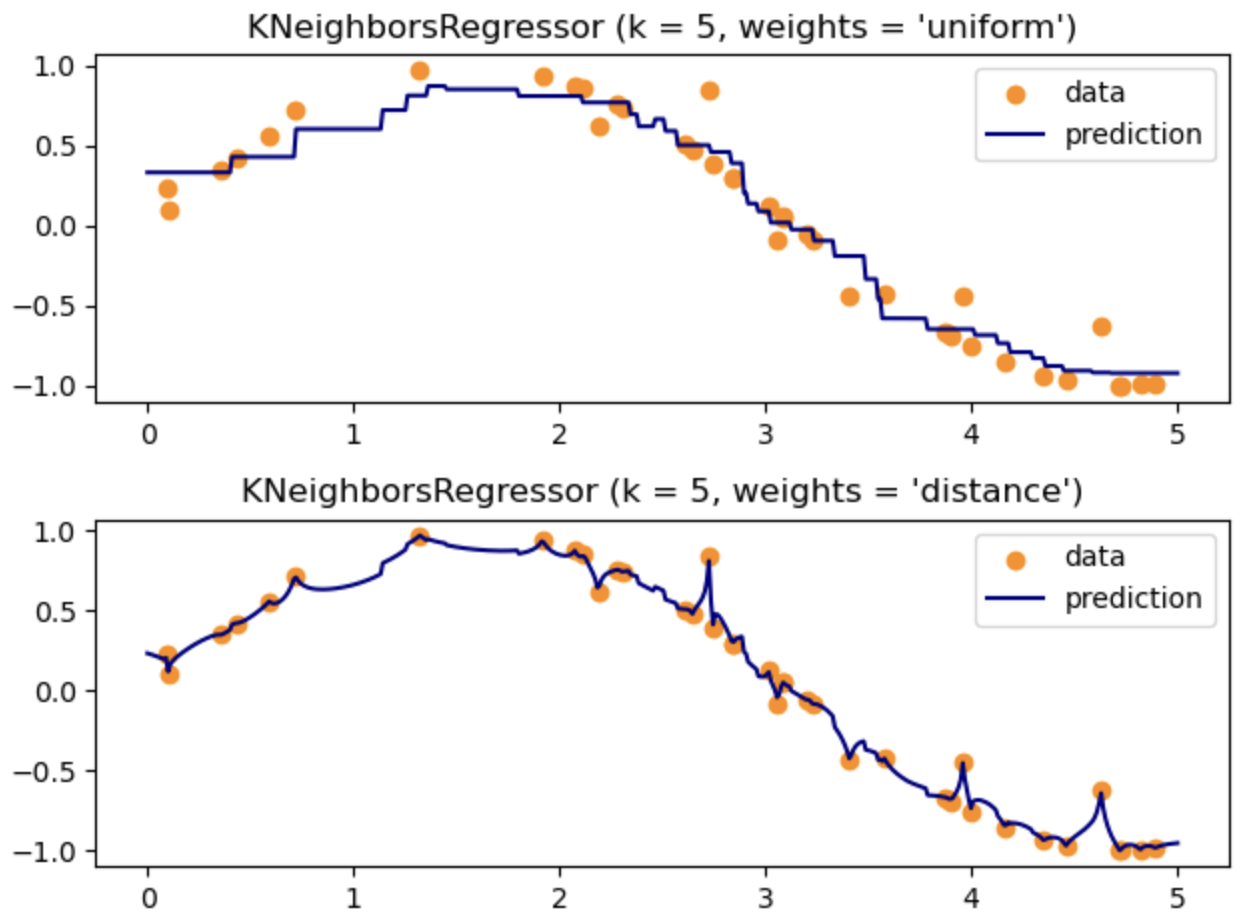
파라미터
weights : ‘uniform’,’distance’
n_neighbors : 이웃의 수 결정
최근접 이웃의 수 증가 ~ 계단의 수 감소, 과소 적합
최근접 이웃의 수 감소 ~ 계단의 수 증가, 과대 적합

'공부' 카테고리의 다른 글
| BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 11장:다층 퍼셉트론 모델 (0) | 2023.12.31 |
|---|---|
| BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 10장: 서포트 벡터 머신 모델 (0) | 2023.12.31 |
| 뉴럴네트워크모델1(구조,비용함수,경사하강법) (0) | 2023.12.29 |
| 오차역전파 (0) | 2023.12.29 |
| BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 5장 : 릿지 회귀 모델 (0) | 2023.12.11 |