
BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 9장: K-최근접
사전지식 : 거리 메트릭 거리 메트릭(distance metric) : 공간에서 두 점 사이의 거리를 측정하는 방법이나 함수를 나타낸다. 민코프스키 메트릭(Minkowski metric) : 유클리드 거리와 맨허탄 거리를 표현
sol-butter1472.tistory.com
9장:KNN 모델 정리
BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 10장: 서포트 벡
BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 9장: K-최근접 사전지식 : 거리 메트릭 거리 메트릭(distance metric) : 공간에서 두 점 사이의 거리를 측정하는 방법
sol-butter1472.tistory.com
10장: SVM 모델 정리
다층 퍼셉트론 모델
사전 지식훑어보기: 확률적 최적화 알고리즘
- 대형 데이터셋에 적용하기 좋은 최적화 기법
- 일부 데이터셋만을 샘플링하는 것이 기본 아이디어

- SGD(확률적 경사 하강법)이 대표적인 알고리즘
- 계산 비용을 절감하며, 비선형 최적화 문제에 대한 솔루션을 빠르게 근사할 수 있다.
- SGD는 수렴 속도가 느리고, 최적화 문제에 따라 최솟값을 찾는 데 어려움이 있을 수 있다.
SGD에서 발전된 알고리즘

Momentum
- SGD보다 빠르게 optimum으로 찾아감 운동량의 개념을 이용하여 gradient를 수정하는 알고리즘 어느 한 방향으로 진행하던 물체의 방향을 바꾸더라도 기존 방향으로 어느정도 힘이 작용하는 것을 나타냄
- 즉, 이전 gradient는 현재 gradient에 영향을 미친다는 개념

- wtij: 현재의 매개변수 값으로, 손실 함수의 기울기에 비례하여 업데이트
- vtij: 모멘텀 벡터의 행과 열 위치, 현재의 기울기 값에 이전 단계의 모멘텀 값을 더한 것
- wt+1ij: 새로운 매개변수 값, 현재의 매개변수에서 모멘텀 값만큼 이동한 값

- t-1시점까지의 이전 움직임들이 각각 베타의 거듭제곱 형태로 반영(β는 하이퍼파라미터)
- 현재 시점의 모멘텀이 계산됨. 지속적으로 누적되는 효과
Adam
- 현재 DNN의 학습에서 가장 광범위하게 이용되고 있는 optimizer
- momentum+RMSProp

- β1: 모멘텀의 지수이동평균 ≈0.9
- β2: 모멘텀의 지수이동평균 ≈0.999
- m^,g^: 학습 초기 시 , 0이 되는 것을 방지하기 위한 보정 값
- ε: 분모가 0이 되는 것을 방지하기 위한 작은 값≈10^-8
- η: 학습율≈0.001
m_t,g_t는 각각 momentum과 RMSProp에서 사용한 수식과 동일
β는 지수이동평균으로써 하이퍼파라미터
지수이동평균은 최근 step의 값을 많이 반영하기 위한 값
다층 퍼셉트론(MLP) 모델

- 생물의 신경망 구조에 착안하여 발전된 신경망 모델
- 기존의 단층 퍼셉트론(입력값의 선형결합 값을 구하고 그 값이 0보다 큰지를 여부로 분류) Boolean XOR 한계 존재(직선으로 구별 불가능) → 다층 퍼셉트론의 등장 계기

XOR 연산은 두 입력 중 정확히 하나가 참(True)일 때 결과가 참이 되며, 그 외의 경우에는 거짓(False)
단층 퍼셉트론에서는 XOR한계로 인해 선형 분리가 불가능했음
다층 퍼셉트론 모델의 구성 요소
- 입력층: 입력변수의 값이 들어오는 곳 , 입력변수의 수 = 입력 노드의 수
- 은닉층: 은닉층에는 다수 노드 포함 가능, 다수의 은닉층 형성 가능
- 출력층: [범주형] 출력 노드의 수 = 출력 변수의 범주 개수 [연속형] 출력 노드의 수 = 출력 변수의 개수
뉴런의 순전파 계산
- 이전 층 뉴런의 선형 결합 수행
- 얻은 값을 토대로 활성화 함수로 변환 후 전달
(입력 신호의 총합을 출력 신호로 변환하는 함수로,
입력 받은 신호를 얼마나 출력할지 결정하고 네트워크에 층을 쌓아 비선형성을 표현)
→ 출력층에 이를 때까지 반복
활성화 함수 종류

활성화 함수에 대한 자세한 설명은 해당 블로그에서 확인
다층 퍼셉트론(MLP) 모델 구현하기

- MLP는 파라미터가 주어졌을 때 오차 역전파를 통해 파라미터 수정
[뉴럴네트워크 파라미터]
파라미터: 층 간 노드를 연결하는 가중치 -> 알고리즘으로 결정
하이퍼파라미터: 은닉층 개수, 은닉노드 개수, activation function ->사용자가 임의로 결정
0단계: 파라미터를 랜덤하게 초기화한다.
구조 설명
1단계: 주어진 파라미터 값에 데이터를 적용하여 예측 클래스 또는 예측값을 계산한다.
2단계: 예측한 클래스나 값과 실제 클래스나 값을 비교한 후 비용 함수를 계산한다.
3단계: 비용 함수를 줄이는 방향으로 1,2단계 반복하며 최적화 진행
1단계: 예측 클래스 또는 예측값을 계산
활성화 함수: 탄젠트 사용(출력 범위 -1~1사이)

입력층→ 첫 번째 은닉층까지 선형 변환 후 활성화 단계 거침
g(W{{1}}^{T}x+b{1})이 출력층으로 가면서 다시 한 번 선형 변환

결국 다층퍼셉트론 모델은 이렇게 이해하면 된다.
x변수들의 선형 결합 -> 선형 회귀 모델
x들의 선형 결합을 로지스틱으로 비선형 변환 -> 로지스틱 회귀 모델
선형 결합의 로지스틱 변환 후 한 번 더 진행 -> 뉴럴네트워크 모델(퍼셉트론)
2단계:비용 함수를 계산
Clssification: cross entropy
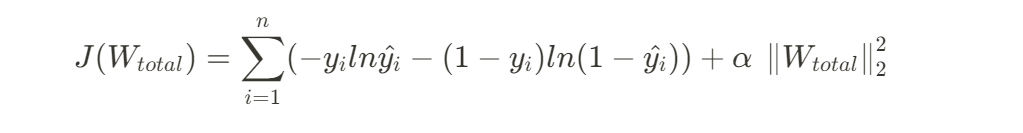
Regression: MSE

3단계: 비용 함수 줄이며 업데이트

이터레이션 단계: t 학습율: ε
시간복잡도

패키지로 표현하기
sklearn.neural_network.MLPClassifier
| 하이퍼파라미터 | 주요값 | 기본값 |
의미 |
| hidden_layer_sizes | tuple | (100,) | 튜플 순서대로 해당 은닉층의 뉴런 수 의미 |
| activation | ‘identity’, ’logistic’, ’tanh’,’relu’ |
‘relu’ | 은닉층에 사용할 활성화 함수 선택 ‘identity’:활성화 과정없이 입력값을 그대로 반환하는 항등 함수 ’logistic’:시그모이드 함수 ’tanh’:하이퍼폴릭 탄젠트 함수 ’relu’:ReLU함수 |
| solver | ‘lbfgs’ ’sgd’,’adam’ |
‘adam’ | 최적화 알고리즘 선택 ’lbfgs’: L-BFGS-B알고리즘 ’sgd’: SBD알고리즘 ’adam’:Adam 알고리즘 |
| alpha | float≥0 | 0.0001 | L2규제항의 계수 |
| batch_size | ‘auto’,int | ‘auto’ | 미니 배치의 크기를 결정하며 확률적 최적화 알고리즘에서만 적용 auto:min(200,n)의 미니 배치 크기 사용 |
| learning_rate_init | float>0 | 0.001 | 확률적 최적화 알고리즘에서의 초기 학습률 |
| max_iter | int>0 | 200 | 에포크의 최대 횟수. |
| shuffle | bool | True | 확률적 최적화 알고리즘에서 이터레이션마다 데이터 셔플링 여부 결정 |
| random_state | int | None | 랜덤성의 제어. 이는 학습 파라미터 초기화 early_stopping이 True일 때의 검증 데이터셋 분할,solver가 sgd나 adam일 경우 배치 추출등에서의 랜덤성을 제어하는 데 사용한다 |
| tol | float | 1e-4 | 학습 조기 종료에 관련된 허용 오차. 손실 함수의 값이나 성능이 n_iter_no_change번의 이터레이션 동안 tol이상만큼 향상하지 않고 learning_rate가 ‘adaptive’가 아닌 경우 학습이 종료된다. |
| early_stopping | bool | False | 확률적 최적화 알고리즘에서만 적용되며, 학습 조기 종료를 판단할 때 검증 데이터셋을 사용할 것인지 선택 True: n_iter_no_change회 에포크 동안 검증 데이터셋에서 tol만큼의 개선이 없다면 학습 조기 종료 False: n_iter_no_change회 에포크 동안 학습데이터셋 전체에서 tol만큼의 개선이 없다면 학습 조기 종료 |
| validation_fraction | 0<float<1 | 0.1 | early_stopping이 True일 때만 적용하며 학습 조기 종료 판단 시 학습 데이터셋 중 검증 데이터셋의 비율 설정 |
| n_iter_no_change | int | 10 | 확률적 최적화 알고리즘에서 tol 개선 여부에 따라 학습 조기 종료를 판단할 에포크의 수 |
SGD 최적화 알고리즘 사용시 하이퍼파라미터
하이퍼파라미터 |
주요값 |
기본값 |
의미 |
| learning_rate | ‘constant’ ’invscaling’ ’adaptive’ |
‘constant’ | 학습률 크기 설정 ‘constant’:learning_rate_init값 계속 적용 ’invscaling’:학습률을 점진적으로 감소 ’adaptive’: 학습 데이터셋의 비용 함수 값이 계속 해서 적절히 감소하는 한 학습률을 learning_rate_init로 유지한다. 연속한 두 에포크에서 학습 데이터셋의 손실이 tol 이하로 감소하지 않거나 early_stopping= True에서 검증 데이터셋 기준 성능이 tol만큼 증가하지 못한다면 현재의 학습률을 1/5배로 감소한다. |
| power_t | float>0 | 0.5 | learning_rate가 ‘invscaling’일 때 학습률의 감쇄 지수 |
| momentum | 0<float≤1 | 0.9 | 경사 하강법을 이용한 파라미터 업데이트에서의 모멘텀 |
| nesterovs_momentum | bool | True | momentum>0일 때만 적용하며 Nesterov모멘텀을 사용할지를 결정 |
Adam 알고리즘 사용시 하이퍼파라미터
| 하이퍼파라미터 | 주요값 | 기본값 | 의미 |
| epsilon | float | 1e-8 | 수치적 안정성 조절 지표 |
| beta_1 | 0≤float<1 | 0.9 | 첫 번째 모멘텀 벡터 추정값의 지수 감쇄율 |
| beta_2 | 0≤float<1 | 0.999 | 두 번째 모멘텀 벡터 추정값의 지수 감쇄율 |
- **solver="adam"**으로 설정됨.
- learning_rate_init 파라미터는 Adam의 초기 학습률을 나타냄.
- 학습 중에 적응적으로 조정되는 학습률 및 지수 가중 이동 평균(moving averages)을 사용하여
- 최적화함.
- 모멘텀과 학습률을 모두 고려하여 안정적이고 빠른 수렴을 도모함
MLPClassifier의 최적화 알고리즘 비교하기
import warnings
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler
from sklearn.neural_network import MLPClassifier
from sklearn.exceptions import ConvergenceWarning
%matplotlib inline
warnings.filterwarnings("ignore")
iris = datasets.load_iris()
X_digits, y_digits = datasets.load_digits(return_X_y=True)
data_sets = [(iris.data, iris.target),(X_digits,y_digits),
datasets.make_circles(noise=0.2, factor= 0.5, random_state =1),
datasets.make_moons(noise=0.3, random_state =0)]labels = ["constant learning-rate", "inv-scaling learning-rate", "adam"]
params = [{
"solver":"sgd",
"learning_rate":"constant",
"momentum": 0,
"learning_rate_init": 0.2
}, {
"solver":"sgd",
"learning_rate":"invscaling",
"momentum": 0,
"learning_rate_init": 0.2
},{ "solver":"adam",
"learning_rate_init":0.01
}]plot_args = [{
"c": "red",
"linestyle":"-"
}, {
"c": "blue",
"linestyle":"-"
}, {
"c":"black",
"linestyle": "-"
}]
def plot_on_dataset(X,y,ax,name):
ax.set_title(name)
X = MinMaxScaler().fit_transform(X)
mlps = []
if name == "digits" : max_iter = 15
else: max_iter = 400
for label, param in zip(labels,params):
mlp = MLPClassifier(random_state=0, max_iter= max_iter, **param).fit(X,y)
mlps.append(mlp)
for mlp,label,args in zip(mlps,labels, plot_args):
ax.plot(mlp.loss_curve_, label=label , **args)
fig, axes = plt.subplots(2,2, figsize = (15,7))
for ax, data, name in zip(axes.ravel(), data_sets,
["iris","digits","circles","moons"]):
plot_on_dataset(*data, ax=ax , name=name)
fig.legend(ax.get_lines(),labels,ncol=3, loc = "upper center")
plt.show()
각 그래프는 이터레이션별 손실값을 표현
- 성능이 좋은 MLP 분류기의 학습 곡선
- Train Loss와 Validation Loss의 수렴:
- 훈련 손실(Train Loss)과 검증 손실(Validation Loss)이 일정 수준 이하로 수렴해야 함
- 초기에는 손실이 크게 감소하다가 안정화되는 지점이 나타나야 함
- Train Accuracy와 Validation Accuracy의 상승:
- 훈련 정확도(Train Accuracy)와 검증 정확도(Validation Accuracy)가 안정적으로 증가
- 훈련 정확도와 검증 정확도가 차이가 크지 않아야 함
- Loss Curve의 부드러운 형태:
- 손실 곡선이 부드럽게 감소해야 함
- 적절한 학습률과 모델 복잡도:
- 학습률이 너무 크면 발산할 수 있고, 너무 작으면 학습이 더디게 진행됨
- 모델이 너무 복잡하면 과적합이 발생할 수 있으며, 너무 단순하면 학습이 충분히 이루어지지 않음
- 적절한 Early Stopping 사용:
- Early Stopping을 통해 검증 손실이 더 이상 감소하지 않을 때 학습을 조기 종료할 수 있음
- 이는 모델이 더 이상 일반화하지 않고 과적합이 시작될 때를 방지

→ MLP는 랜덤성과 하이퍼파라미터에 따라 모델의 성능이 변화함
결론
- MLP 모델의 최적화 결과는 피처 스케일링 여부에 예민함
- 모든 비선형 모델 학습이 가능하며 성능이 우수하게 나온다는 장점
- 은닉층이 많으면 많을수록 학습 시간이 오래 걸리고 과적합 발생 가능성의 단점
- 은닉층이 있는 MLP 비용함수는 컨벡스 함수가 아니므로 지역 최솟값이 여러 개 발생
- 최적화에서 초깃값에 따라 서로 다른 여러 가지 해를 얻을 수 있다는 단점
참고
SGD https://sjpyo.tistory.com/56
손실함수 최적화에서 모멘텀의 필요성 https://mole-starseeker.tistory.com/67
활성화 함수 https://heeya-stupidbutstudying.tistory.com/entry/ML-활성화-함수Activation-Function
'공부' 카테고리의 다른 글
| [데밸첼 4기] 그로스 해킹 (그로스해킹이란?/전제조건/AARRR) (1) | 2024.11.09 |
|---|---|
| [BDA x 이지스 퍼블리싱] Easy Study Project 마무리를 하며 (0) | 2024.01.26 |
| BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 10장: 서포트 벡터 머신 모델 (0) | 2023.12.31 |
| BDA X 이지스퍼블리싱 서평단 이벤트 [Do it! 데이터 과학자를 위한 실전 머신러닝]/ 9장: K-최근접 이웃 모델 (0) | 2023.12.31 |
| 뉴럴네트워크모델1(구조,비용함수,경사하강법) (0) | 2023.12.29 |